Project: Complex Numbers#

Complex numbers are expressed in the form \(a+bi\) where a and b are real numbers, and i is the imaginary unit defined by \(i=\sqrt{-1}\).

In this expression, \(a\) is referred to as the real part of the complex number, while \(b\) is the imaginary part.

Basics#

List Representation#

Complex numbers can also be represented as an ordered pair \([a,b]\), where the first element corresponds to the real part and the second to the imaginary part.

\(a+bi \rightarrow [a,b]\)

def complex_list(real, imaginary):
    return [real, imaginary]

print(complex_list(2,3))

[2, 3]

String Representation#

Complex numbers can also be represented as strings.

  • Unlike standard positive numbers, when representing complex numbers with a positive imaginary part, a + sign must be explicitly included between the real and imaginary parts (e.g., “3+4i”).

  • However, if the imaginary part is negative, the minus sign is included automatically (e.g., “3-4i”), so there is no need to add it manually.

def complex_str(complex_num):
    if complex_num[1] >= 0:
        return str(complex_num[0]) + '+'  + str(complex_num[1]) + 'i'
    else:
        return str(complex_num[0]) +  str(complex_num[1]) + 'i'

complex_str([2,3])

'2+3i'

complex_str([2,-3])

'2-3i'

complex_str([2,0])

'2+0i'

Conjugation#

The conjugate of a complex number has the same real part but the opposite sign of the imaginary part.

  • Conjugate of \(2+3i\) is \(2-3i\).

  • Conjugate of \(5-7i\) is \(5+7i\).

def complex_conjugate(complex_num):
    return [complex_num[0], -complex_num[1]]

print(complex_conjugate([2,3]))

[2, -3]

print(complex_conjugate([5,-7]))

[5, 7]

Graphical Representations#

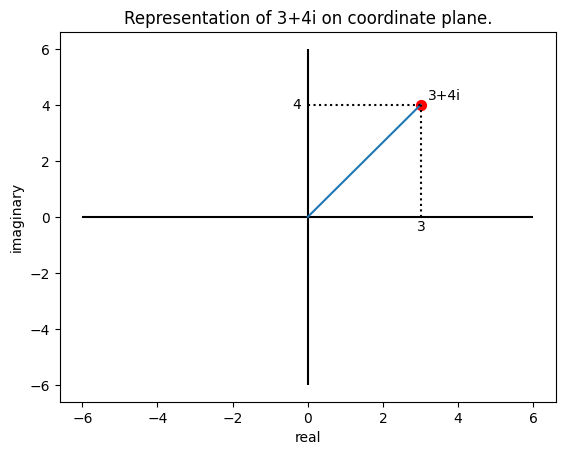
Complex numbers can be represented on the coordinate plane, where the horizontal axis (x-axis) corresponds to the real part and the vertical axis (y-axis) corresponds to the imaginary part.

\(a+bi \rightarrow (a,b)\)

import matplotlib.pyplot as plt
def plot_complex(complex_num):
    a, b = complex_num
    boundary = max(a, b)+2

    plt.vlines(0, -boundary, boundary, color='k' )
    plt.hlines(0, -boundary, boundary, color='k' )

    plt.plot([0, a], [0, b])
    plt.scatter(a, b, c='red', s=50)

    plt.text(a+.2, b+.2, complex_str(complex_num))
    plt.text(a-0.1, -0.5, a)
    plt.text(-0.4, b-0.15, b)

    plt.vlines(a, 0, b, color='k', linestyle='dotted')
    plt.hlines(b, 0, a, color='k', linestyle='dotted' )

    plt.xlabel('real')
    plt.ylabel('imaginary')
    plt.title(f'Representation of {complex_str(complex_num)} on coordinate plane.')

plot_complex([3,4])
_images/7fb08740b115c96d9a43513fe564bc34f9ca4066af30188bd1a0d978a2631132.png

Absolute Value (Modulus)#

The absolute value (or modulus) of a complex number is the distance between the complex number and the origin in the complex plane.

\(|a+bi| = \sqrt{a^2+b^2}\)

import math

def complex_abs(complex_num):
    return math.sqrt(complex_num[0]**2 + complex_num[1]**2)

complex_abs([3,4])

5.0

Quadrants#

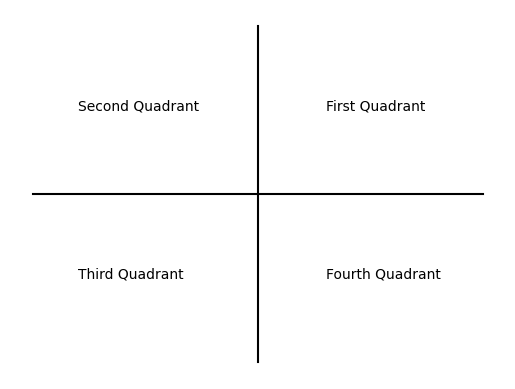
The coordinate plane is divided into four quadrants, each defined by the signs of the \(x\) and \(y\) coordinates:

  • First Quadrant: \(x>0,\,\, y>0\)

  • Second Quadrant: \(x<0,\,\, y>0\)

  • Third Quadrant: \(x<0,\,\, y<0\)

  • Fourth Quadrant: \(x>0,\,\, y<0\)

Quadrant

x

y

First

+

+

Second

-

+

Third

-

-

Fourth

+

-

 
plt.plot([-5,5], [0,0], c='k')
plt.plot([0,0], [-5,5], c='k')

plt.text( 1.5, 2.5, 'First Quadrant' )
plt.text(-4, 2.5, 'Second Quadrant' )
plt.text(-4, -2.5, 'Third Quadrant' )
plt.text( 1.5, -2.5, 'Fourth Quadrant' )

plt.axis('off');
_images/e78c8e00c6467d75acf689e36b365d838001fdf8564bc538e621da568435f2c8.png 
def complex_quadrant(complex_num):
    if (complex_num[0] > 0) & (complex_num[1] > 0):
        return 1
    elif (complex_num[0] < 0) & (complex_num[1] > 0):
        return 2
    elif (complex_num[0] < 0) & (complex_num[1] < 0):
        return 3
    elif (complex_num[0] > 0) & (complex_num[1] < 0):
        return 4
    else:
        return 'Not in a quadrant'

print(complex_quadrant([-2,3]))

2

print(complex_quadrant([-2,0]))

Not in a quadrant

print(complex_quadrant([-2,-3]) )

3

Algebraic Operations#

Addition#

The sum of two complex numbers is obtained by adding their real parts and their imaginary parts separately.

  • \((a + b i) + (c + d i) = (a+c)+(b+d)i \)

  • \([a, b] + [c, d] = [a+c,\,\, b+d] \)

Example: [1,4] + [5,8] = [1+5, 4+8] = [6, 12]

def complex_add(complex1, complex2):
    real = complex1[0]+complex2[0]
    imaginary = complex1[1]+complex2[1]
    return [real, imaginary ]

print(complex_add([1,4], [5,8]))

[6, 12]

Subtraction#

The difference of two complex numbers is found by subtracting their real parts and their imaginary parts separately.

  • \((a + b i) - (c + d i) = (a-c)+(b-d)i \)

  • \([a, b] - [c, d] = [a-c,\,\, b-d] \)

Example: [10,4] - [7,8] = [10-7, 4-8] = [3,-4]

def complex_subtract(complex1, complex2):
    real = complex1[0]-complex2[0]
    imaginary = complex1[1]-complex2[1]
    return [real, imaginary ]

print(complex_subtract([10,4], [7,8]))

[3, -4]

Multiplication#

The product of two complex numbers is calculated using the distributive property, along with the identity \(i^2=-1\).

  • \((a+bi)\cdot (c+di) = (ac-bd)+(ad+bc)i\)

  • \([a,b]\cdot [c,d] = [ac-bd, ad+bc]\)

Example: \([1,3]\cdot [2,5] = [1\cdot 2-3\cdot 5, 1\cdot 5 + 2\cdot 3]= [2-15, 5+6] = [-13, 11]\)

def complex_multiply(complex1, complex2):
    real = complex1[0]*complex2[0] - complex1[1]*complex2[1]
    imaginary = complex1[0]*complex2[1] + complex1[1]*complex2[0]
    return [real, imaginary ]

print(complex_multiply([1,3], [2,5]))

[-13, 11]

Division#

Division of complex numbers is performed by multiplying both the numerator and the denominator by the conjugate of the denominator. This process eliminates the imaginary part from the denominator, converting it into a real number.

\(\displaystyle \frac{a+bi}{c+di} = \frac{(a+bi)\cdot(c-di)}{(c+di)\cdot(c-di)}\frac{(a+bi)\cdot(c-di)}{|c+di|^2} = \frac{(a+bi)\cdot(c-di)}{c^2+d^2} \)

      \( \displaystyle = \frac{(ac-bd)+(ad+bc)i}{c^2+d^2} = \frac{ac-bd}{c^2+d^2}+\frac{ad+bc}{c^2+d^2}i\)

  • \(\displaystyle \frac{[a,b]}{[c,d]} = \frac{[a,b]\cdot[c,-d]}{[c,d]\cdot[c,-d]} = \frac{[ac-bd, ad+bc]}{[c^2+d^2, 0]}= \left[\frac{ac-bd}{c^2+d^2}, \frac{ad+bc}{c^2+d^2}\right]\)

Example: \(\displaystyle\frac{[1,2]}{[3,4]} = \frac{[1,2]\cdot[3,-4]}{[3,4]\cdot[3,-4]} = \frac{[1\cdot 3- 2\cdot (-4),1\cdot(-4)+2\cdot 3]}{3^2+(-4)^2}= \frac{[11,2]}{25} =\left[\frac{11}{25}, \frac{2}{25}\right] = [0.44, 0.08]\)

def complex_division(complex1, complex2):
    num_list = complex_multiply(complex1, complex_conjugate(complex2))
    den = complex_abs(complex2)**2
    return [num_list[0]/den, num_list[1]/den ]

print(complex_division([1,2], [3,4]))

[0.44, 0.08]

Reciprocal#

The reciprocal of a complex number is found by dividing 1 by the number.

  • \(\displaystyle \frac{1}{[a,b]} = \frac{[1,0]}{[a,b]}\)

def complex_reciprocal(complex_num):
    return complex_division([1,0], complex_num)

print(complex_reciprocal([3,4]))

[0.12, -0.16]

Exponentiation#

To find the \(n\)th power of a complex number, multiply the complex number by itself \(n\) times.

def complex_power(complex_num, power):
    result = [1,0]
    for i in range(power):
        result = complex_multiply(result, complex_num)
    return result

print(complex_power([2,3], 10))

[-341525, -145668]

Let’s find \(i^{10}\) using the following fact:

  • \( i = 0+1i = [0,1]\)

print(complex_power([0,1], 10))

[-1, 0]

Future Work#

Write a Python program that visualizes the powers of a given complex number \(a+bi\) on the complex plane. The program should:

  • Take a complex number as a list and an integer \(n\)

  • Compute and plot the first \(n\) powers of \(a+bi: (a+bi)^1, (a+bi)^2, (a+bi)^3,...,(a+bi)^n\)

  • Display each point on the complex plane and connect them in order to show the trajectory.

  • Label each point with its power \((a+bi)^1, (a+bi)^2, (a+bi)^3,...,(a+bi)^n\)