Variables Exercises#

Section Title: Variables Exercises

Question-1: Name Tag#

Use the following information to create the variables name, league, age, and height with the given values.

  • Create the birthyear variable using the age variable.

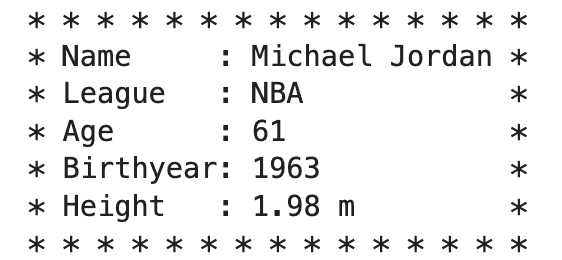
  • Design a name tag as given below.

  • There is a space between each asterisk in the first and last lines.

Michael Jordan played basketball in the NBA. In 2024, he is 61 years old, and his height is 1.98 meters.

Sample Output:

A rectangular frame made of asterisks that includes the following text:Name : Michael JordanLeague : NBAAge : 61Birthyear: 1963Height : 1.98 m

Question-2: Repeating Digits#

By using the variables \(x\) and \(y\) given below, print 353535 using 4 different pieces of code.

x, y = 3, 5

Question-3: Sentence Builder#

Print the statement I went to Italy in 2015. using the country and year variables below.

country = 'Italy'
year = 2015

Warning: There is no space before the period.

Question-4: Circle#

Create a variable named r and assign the value of \(5\) to it.

  • Print the area and perimeter of the circle with a radius equal to r.

  • Round them to the nearest hundredth.

  • Hint:

    • Perimeter = \(2\pi r\), Area = \(\pi r^2\)

    • Import \(\pi\) from a module.

  • Output:

    • Perimeter: 31.42

    • Area : 78.54

Question-5: U-Shape#

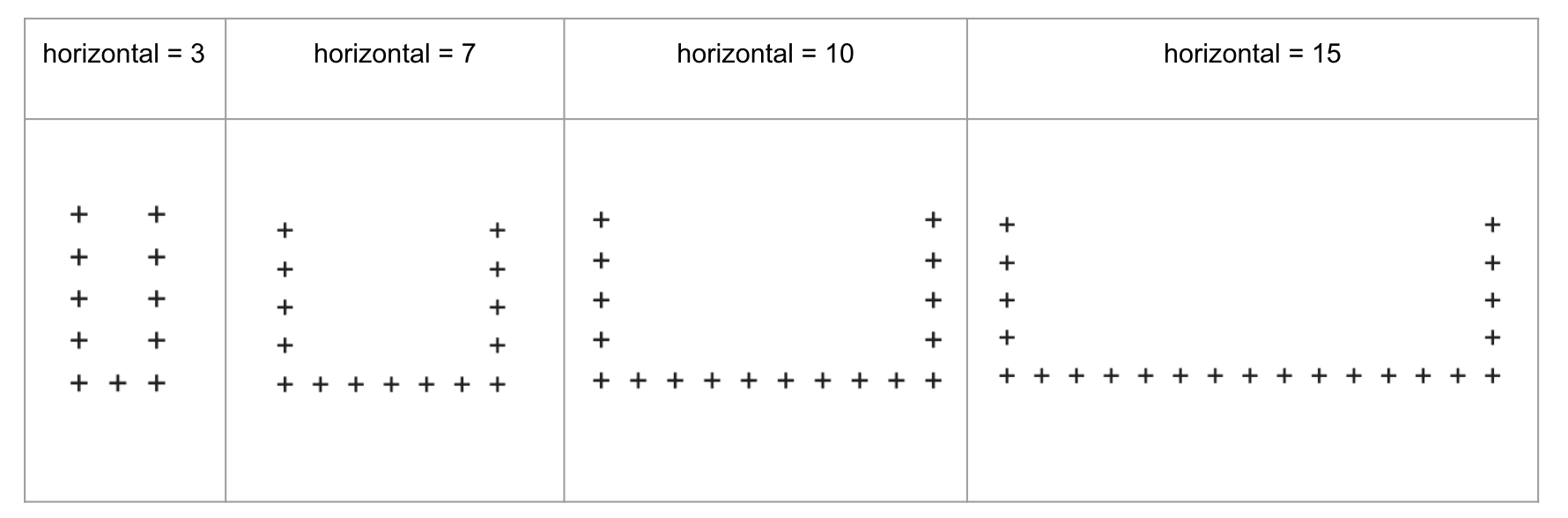
Print the letter U using the character + and the variable horizontal.

horizontal = 3

  • The vertical left and right parts of U have five + characters each.

  • The variable horizontal represents the number of + characters with one space between them in the bottom horizontal part.

Examples The U shape is formed using + characters. The first four rows each contain two + characters with a varying number of spaces between them, depending on the horizontal variable's value. The final row (fifth) contains a number of + characters equal to the horizontal variable's value, with one space separating each +.

Question-6: V-Shape#

Print the following using the character *, spaces and the variable n=5 to represent the number of * characters in each block.

In the first row, there are two blocks of n stars with 7n spaces between them.In the second row, there are two blocks of n stars with 5n spaces between them.In the third row, there are two blocks of n stars with 3n spaces between them.In the fourth row, there are two blocks of n stars with n spaces between them.In the fifth (last) row, there is a single block of n stars.

Question-7: H-Shape#

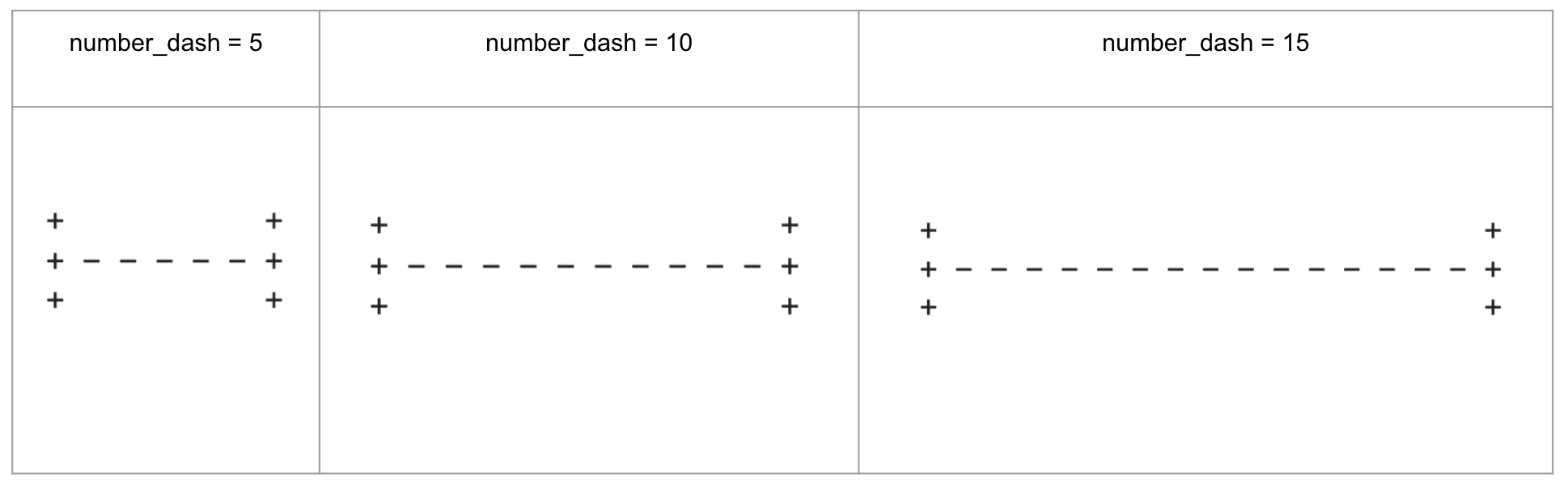
Print the following ‘H’ shapes using the characters ‘+’, ‘ ‘, ‘-’, and the variable number_dash.

number_dash = 5

  • The number of ‘-’ characters in the middle line is represented by the variable ‘number_dash’.

Examples In the first and third (last) rows, there are two + characters with a certain number of spaces between them, depending on the number_dash variable. In the second row, there are two + characters with a certain number of dashes between them, also determined by the number_dash variable. There is a spaceafter each dash.

Question-8: Receipt Generator#

The following code generates a basic store receipt. Improve its appereance by adding separators (dashes -) and formatting the price, tax, tip, and discount details to make it look more professional, similar to real receipts.

from datetime import datetime
current_date_time = datetime.now().strftime('%Y-%m-%d %H:%M:%S')  # string object

restaurant_name = 'Olive Garden'
price = 100  
tax = 0.08
tip = 0.15
discount = 7

tax_amount = tax*price
tip_amount = tip*price

total = price + tax_amount + tip_amount - discount

print(restaurant_name) 
print(current_date_time)
print('Total          :', total)

Question-9: Dynamic Arrow#

Define a variable called num_dashes and set it equal to 5.
Using this variable, generate an arrow that consists of:

  • num_dashes number of dashes (-)

  • followed by a greater than sign (>)

Print the arrow.

  • Example Output (when num_dashes = 5): —–>

Question-10: Print Variables#

Define the following variables with appropriate values and print them in one sentence:

  • first_name

  • last_name

  • age

  • state

Example output format: My name is Michael Bird. I am 45 years old and live in New York.

Question-11: Temperature Conversion#

Define a variable called celsius and set it to 25.
Convert it to Fahrenheit using the formula:

  • \(\displaystyle F = \frac{9}{5}C+32\)

Print the result

  • Example output format: 25 C = 77.0 F

Question-12: Symbol Square#

Define a variable symbol and set it to ‘*’.
Define a variable count and set it to 7.
Print a square of size count × count using the symbol variable.
Hint: Use \n to create new lines.

Question-13: Swap Digits#

Define a variable called number and assign it any two-digit integer (e.g., 47).
Swap the tens and ones digits of the number.
Store the result in a new variable called swapped_number.
Print the original number and the swapped number in a clear sentence.

Example Output:

  • Original number: 47

  • Swapped number: 74

Hint:

  • To extract the tens digit: tens = number // 10

  • To extract the ones digit: ones = number % 10

  • To combine them in swapped order: swapped_number = ones * 10 + tens

Question-14: String Operations#

Define three variables: first, middle, and last.
Generate an email in the format: first.middle.last@nba.com

  • All lowercase (use the lower() method of strings)

  • Replace spaces with underscores (use the replace method of strings)

Display the results as: