Chp-9: Functions

Chp-9: Functions#

Chapter Objectives

By the end of this chapter, the student should be able to:

Explain the purpose and role of functions.
Define and call functions with and without parameters and return statements.
Use local and global variables effectively.
Perform recursion.
Write and interpret docstrings.
Apply functions to solve real-world problems.

Motivation#

We have seen the following code related to the grading scale in the Conditionals chapter.

It displays the corresponding letter grades according to the following chart.

Letter Grade	Grade Range
A	80 - 100
B	60 - 79
C	40 - 59
D	20 - 39
F	0 - 19

grade = 90

if 80 <= grade <= 100:
    print('Your letter grade is A')
elif 60 <= grade :
    print('Your letter grade is B')
elif 40 <= grade :
    print('Your letter grade is C')
elif 20 <= grade :
    print('Your letter grade is D')
elif 0 <= grade :
    print('Your letter grade is F')
else:
    print(f'{grade} is not a percent grade')

Your letter grade is A

If you need the letter grades for more than one student in your program, copying and pasting this code multiple times with different grade values will make your program very lengthy and hard to read.

Instead, you can use a function, similar to functions in mathematics, which takes grade as input and prints the corresponding letter grade.
The function version is as follows and displays letter grades for three students.

# this is the function named letter_grade
def letter_grade(grade):
    if 80 <= grade <= 100:
        print('Your letter grade is A')
    elif 60 <= grade :
        print('Your letter grade is B')
    elif 40 <= grade :
        print('Your letter grade is C')
    elif 20 <= grade :
        print('Your letter grade is D')
    elif 0 <= grade :
        print('Your letter grade is F')
    else:
        print(f'{grade} is not a percent grade')    

# call function
letter_grade(80)
letter_grade(50)
letter_grade(30)

Your letter grade is A
Your letter grade is C
Your letter grade is D

As you can see above, you just need to call the function by its name with the input value.
This makes the code short and easy to read.

Functions#

Functions are used to avoid repetitions in a program by constructing reusable code.

By using functions, a long code can be split into multiple functions like Lego bricks.
In this way, it becomes easy to read and understand the code.
A function can be called in a program with its name and parameters, and functions can include print statements.

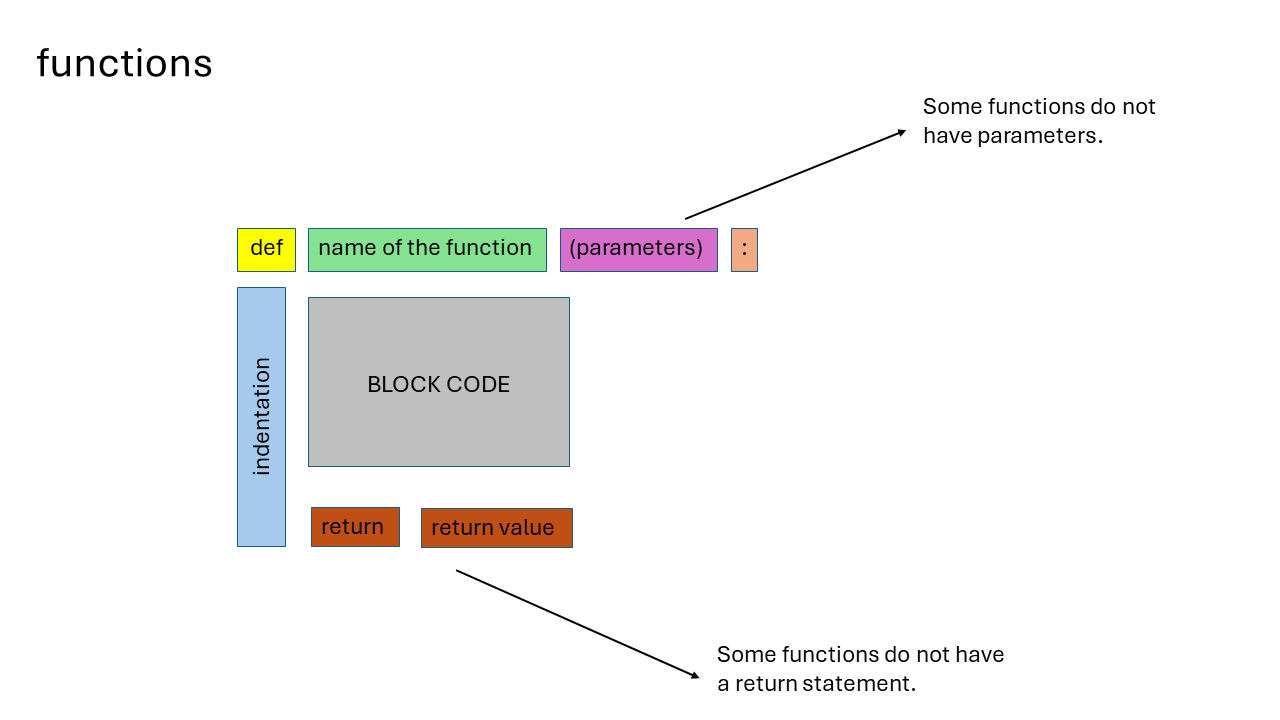
The structure of a function is as follows:

def function_name(parameters):

BLOCK CODE

return return_value

In the structure above:

def is a keyword that initiates the construction of the function.
function_name is the name of the function used to call it.
- It is a good practice to choose meaningful names for functions to remember their purpose.
parameters are the comma-separated inputs of the function.
- A function can have no parameters, one, or more parameters.
: comes right after the parameters, indicating that the following lines will be part of the function’s code block.
BLOCK CODE is a group of code with the same indentation level that will be executed with the given parameter values.
return is a keyword that terminates the function.
return_value is the output of the function.
- Some functions may not have a return statement.

Example: Square Function

The following function is named \(f\).

Its parameter is \(x\) (a number).
It calculates the square of \(x\).
It returns the square as its output.

def f(x):
  square = x**2
  return square

# call the function for x=3
print(f(3))

# call the function for x=5
print(f(5))

Example: Area of a Rectangle

The following function is named area_rect.
It has two parameters: width and height.
It calculates the area using the formula \(Area = Width \times Height\).
It returns the area as its output.

def area_rect(width, length):
  area = width*length
  return area

# call the function for width=5, height=10
print(area_rect(5, 10))

# call the function for width=8, height=9
print(area_rect(8,9))

Example: Rational Function

Consider the function \(\displaystyle f(x) = \frac{x^2+3}{x^3+2x-1}\)
The function takes one parameter: \(x\).
It calculates the numerator and denominator separately, then computes their quotient.
The function returns the resulting quotient.

def f(x):
    numerator = x**2+3
    denominator = x**3+2*x-1
    quotient = numerator/denominator
    return quotient

# call the function for x=2
print(f(2))

0.6363636363636364

Example: Area and Perimeter of a Circle

The following function is named circle_area_perimeter.
It has one parameter: radius.
It calculates the area and perimeter of a circle with radius \(r\) using the formulas: \(area = \pi r^2\) and \(perimeter = 2\pi r\).
The calculated area and perimeter are rounded to the nearest hundredths.
The function returns the tuple (area, perimeter) as its output.

import math

def circle_area_perimeter(radius):
  area = math.pi*radius**2
  perimeter = 2*math.pi*radius
  area_round = round(area, 2)
  perimeter_round = round(perimeter, 2)
  return (area_round, perimeter_round)

# call the function for radius=5
print(circle_area_perimeter(5))

(78.54, 31.42)

# call the function for radius=10
print(circle_area_perimeter(10))

(314.16, 62.83)

The function returns a dictionary containing both the area and the perimeter.

def circle_area_perimeter_dict(radius):
  area = math.pi*radius**2
  perimeter = 2*math.pi*radius
  area_round = round(area, 2)
  perimeter_round = round(perimeter, 2)
  return {'area': area_round, 'perimeter': perimeter_round}

print(circle_area_perimeter_dict(10))

{'area': 314.16, 'perimeter': 62.83}

Example: Fahrenheit to Celcius Converter

The following function is named conv_f_c.
It has one parameter: fahrenheit.
It calculates the equivalent Celsius value using the conversion formula: \(celsius = \frac{(fahrenheit - 32)}{1.8}\).
The Celsius value is rounded to the nearest hundredths.
The function returns the Celsius value

def conv_f_c(fahrenheit):
  celcius = (fahrenheit-32)/1.8
  celcius_round = round(celcius, 2)
  return celcius_round

# call the function for fahrenheit=100
print(conv_f_c(100))

37.78

# call the function for fahrenheit=20
print(conv_f_c(20))

-6.67

No return statement#

It is possible to have functions with no return statement.
Such functions usually include print statements.

The following function takes a name as its input and then prompts for the age.

def age(name):
  print(f'How old are you {name}?')

age('Arthur')

How old are you Arthur?

If you run the following code:
- The print statement will be executed.
- Since there is no return statement, no value will be returned, and x will be of type NoneType.

x = age('Arthur')

How old are you Arthur?

print(x)

None

print(type(x))

<class 'NoneType'>

No parameters#

It is possible for a function to have no parameters.

def welcome():
    greeting = '''Good morning everyone,
I hope you are all doing well. It's a great pleasure for me to wellcome all of you to today's meeting. 
We have a very busy schedule today. Let's start working on each subject one by one. Thank you for being here!'''
    return greeting

print(welcome())

Good morning everyone,
I hope you are all doing well. It's a great pleasure for me to wellcome all of you to today's meeting. 
We have a very busy schedule today. Let's start working on each subject one by one. Thank you for being here!

Default parameter values#

If no value is given to the parameter, the default value will be used.

Default values are typically assigned to parameters that are not frequently used or have a common default value.
Non-default parameters should precede default parameters.

# course parameter has a default value

def student_report(name, grade, course='Math'):
  print(f'{course} grade of {name} is {grade}.')

# call student_report of Michael for CS 

student_report('Michael', 87, 'CS')

CS grade of Michael is 87.

# course value is not given so default value='Math' is used

student_report('Michael', 87)

Math grade of Michael is 87.

# ERROR: Default parameter course cannot come before non-default parameter grade

def student_report(name, course='Math', grade):
  print(f'{course} grade of {name} is {grade}.')

Local and Global Variables#

Local variables are defined inside a function and can only be accessed within that function.
Global variables are defined outside a function and can be accessed inside a function, but they cannot be modified within the function.
- When a global variable is called, a new local variable is used.

a = 4     # global variable

def f(x):
    b = 5   # local variable
    result = a+b+x
    return result

# call function for x=10
print(f(10))

# you can access 'a' outside the function: global variable
print(a)

# ERROR: 'b' is not defined outside the function: local variable
print(b)

# ERROR: 'result' is not defined outside the function: local variable
print(result)

a = 4     # global variable

def f(x):
    a = 100       # change the value of a
    b = 5   
    result = a+b+x
    return result

# call function for x=10
print(f(10))   # a=100 is used 

# The value of 'a' outside the function has not been changed
print(a)

Recursions#

Recursion in programming refers to when a function calls itself.

It’s an efficient way to solve complex problems by breaking them down into smaller, more manageable tasks.
It uses patterns to simplify complex tasks.
By using recursion, functions can tackle large tasks step by step, making the code more concise and efficient.

In the following example, the function sum_func calculates the sum of integers from 1 to a given positive integer n using a for loop.

def sum_func(n):
    total = 0
    for i in range(1, n+1):
        total += i
    return total

sum_func(5)

In the following code, the function sum_func calculates the sum of integers from 1 to a given positive integer n using recursion.

In the last line, the function sum_func_rec calls itself within itself.
The condition n == 0 is the base case, stopping the recursion to prevent infinite execution.

def sum_func_rec(n):
    if n == 0:
        return 0
    else:
        return n + sum_func_rec(n-1)

sum_func_rec(5)

Let’s proceed step by step:

When sum_func_rec(5) is called, the block code of the function sum_func_rec is executed for n=5.
- Since n=5 is not zero, the else part is executed, and we have sum_func_rec(5) = 5+sum_func_rec(4).
When sum_func_rec(4) is called, the block code of the function sum_func_rec is executed for n=4.
- Since n=4 is not zero, the else part is executed, and we have sum_func_rec(4) = 4+sum_func_rec(3).
When sum_func_rec(3) is called, the block code of the function sum_func_rec is executed for n=3.
- Since n=3 is not zero, the else part is executed, and we have sum_func_rec(3) = 3+sum_func_rec(2).
When sum_func_rec(2) is called, the block code of the function sum_func_rec is executed for n=2.
- Since n=2 is not zero, the else part is executed, and we have sum_func_rec(2) = 2+sum_func_rec(1).
When sum_func_rec(1) is called, the block code of the function sum_func_rec is executed for n=1.
- Since n=1 is not zero, the else part is executed, and we have sum_func_rec(1) = 1+sum_func_rec(0).
When sum_func_rec(0) is called, the block code of the function sum_func_rec is executed for n=0.
- The condition of the if statement is True, so it returns 0, meaning sum_func_rec(0) = 0
- We’ve reached the base case and will now backtrack.
sum_func_rec(1) = 1 + sum_func_rec(0) = 1 + 0 = 1
sum_func_rec(2) = 2 + sum_func_rec(1) = 2 + 1 = 3
sum_func_rec(3) = 3 + sum_func_rec(2) = 3 + 3 = 6
sum_func_rec(4) = 4 + sum_func_rec(3) = 4 + 6 = 10
sum_func_rec(5) = 5 + sum_func_rec(1) = 5 + 10 = 15

DocStrings#

Docstrings are strings declared within a function to describe the purpose and functionality of that function.

They can be accessed using the doc attribute of the function, like so: function_name.doc.

def area_rect(width, length):
    
    ''' Calculates area of a rectangle. 
    
    Parameters
    ----------
    width: float 
       The width of the rectangle.

    length: float 
       The length of the rectangle.
    
    Returns
    -------
    float
        The area of the rectangle.
    '''

    
    area = width * length
    return area

print(area_rect(5, 10))

print(area_rect.__doc__)

 Calculates area of a rectangle. 
    
    Parameters
    ----------
    width: float 
       The width of the rectangle.

    length: float 
       The length of the rectangle.
    
    Returns
    -------
    float
        The area of the rectangle.
    

Lambda Function#

The lambda function allows for the creation of functions in a more concise manner.

It is in the form of:

name_of_the_function = lambda variables: expression

lambda is a keyword.
variables can be multiple, separated by commas.

Example: Square Function

square_func = lambda x: x**2 

print(square_func(5))

Example: Area of a rectangle

rect_area = lambda width, length: width*length 

print(rect_area(5, 10))

Examples#

Calculator#

Write a function whose parameters are two numbers and a string (operation)

Operations are given as strings in the form of '+', '*', '/', '-'
By using the given numbers and operation find number1 operation number2
If the operation is division second parameter (denominator) can not be zero and display a warning message.
If the operation is not one of the four operations given above display a warning message.

def calculator(number1, number2, operation):
    
  if operation == '+':
    return number1 + number2
  elif operation == '-':
    return number1 - number2
  elif operation == '*':
    return number1 * number2
  elif operation == '/':
    if number2 == 0:
      print('Warning: zero division')
    else:
      return number1/number2
  else:
    print(f'{operation} is not an available operation.')

# addition
print(calculator(7,2,'+'))

# subtraction
print(calculator(7,2,'-'))

# multiplication
print(calculator(7,2,'*'))

# division
print(calculator(7,2,'/'))

3.5

# division by zero
calculator(7,0,'/')

Warning: zero division

# inappropriate operation
calculator(7,3,'%')

% is not an available operation.

Factorial#

Factorial is a mathematical operation denoted by an exclamation mark (!) next to a positive integer.

It represents the product of all positive integers up to that number.
The factorial of 5, written as 5!, equals 5 × 4 × 3 × 2 × 1.
By definition, 0! = 1

Write a function that takes a non-negative integer as input and computes its factorial.

# use a for loop
def factorial(n):
    product = 1
    for i in range(1, n+1):
        product *= i
    return product

print(factorial(5))

# use a recursion
def factorial_rec(n):
    if n == 1:
        return 1
    else:
        return n*factorial_rec(n-1)

print(factorial_rec(5))