Functions Exercises#

Section Title: Functions Exercises

Question-1: Harmonic Mean#

Write a function that takes three numbers as parameters and returns the harmonic mean of these numbers using the formula: \(\displaystyle H(x, y, z) = \frac{3}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}\).

Question-2: Circle#

Write a function that takes two parameters: radius (\(r\)) with a default value of 1, and calculation_type with a default value of “area”.

  • If calculation_type is area (\(\pi r^2\)) the function returns the area of the circle, rounded to the nearest hundredth.

  • If calculation_type is perimeter(\(2\pi r\)) the function returns the perimeter of the circle, rounded to the nearest hundredth.

  • If calculation_type is both the function returns a tuple containing both the perimeter and the area of the circle, each rounded to the nearest hundredth.

  • If calculation_type is anything else, it prints a “not valid type” warning.

Question-3: Algebraic Operations#

Write a function that takes two numbers as parameters and returns the results of the four basic operations.

  • If the second number is zero for division, print a warning message about division by zero.

  • Round the result of the division to the nearest hundredth.

Sample Output: alg_operation(3,7)

3 + 7 = 10
3 - 7 = -4
3 x 7 = 21
3 / 7 = 0.43

Question-4: Letters#

Write a function that takes a number as its input and returns the first corresponding number of lowercase letters from the alphabet.

  • If the input number exceeds the total number of letters in the alphabet, the function returns all letters.

  • If the input is zero or negative, it returns an empty string.

Sample Output

print(letter_func(4))
abcd

print(letter_func(-5))
(No Output)

print(letter_func(40))
abcdefghijklmnopqrstuvwxyz

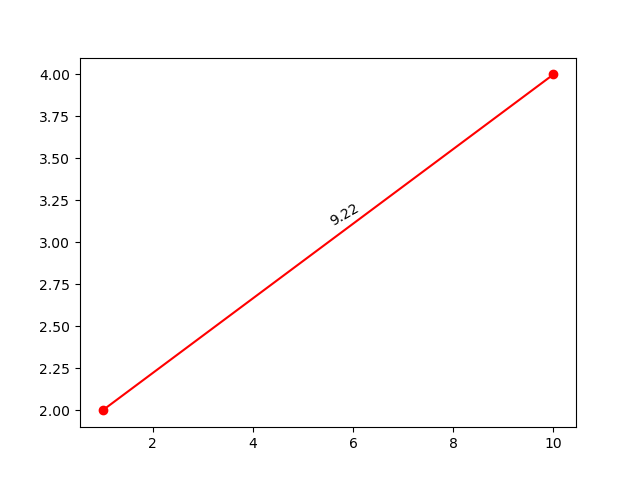
Question-5: Distance#

Write a function that takes four parameters: the (x, y) coordinates of two points, A and B.

  • Plot a red line connecting these two points on a graph.

  • Label points A and B by adding texts next to each point.

  • Calculate the distance between these points and display it as text in the middle of the line.

  • Rotate the text for better visibility.

Sample Output

This is a plot featuring a red line segment connecting two points, with the distance between these two points measuring 9.22 units. This distance is indicated in th emiddle of the line segment on the plot.

Question-6: Password Check#

Select a 4-digit password. Then, write a function that takes a 4-digit number as its parameter.

  • If the provided number is within 10 units of the chosen password, the function should print a message granting permission to enter; otherwise, it should print a message denying entrance.

Sample Output

password_check(1234)
DENY!

password_check(4325)
ACCEPT!

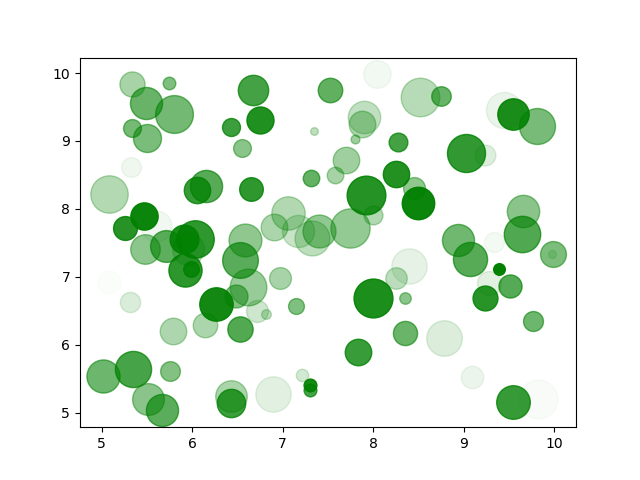
Question-7: Random Points#

Write a function that takes a parameter representing the number of points to plot in green.

  • This function should generate random points, each with random sizes and transparencies, and plot them on a graph.

  • The sizes of the points should be integers ranging from 5 to 800.

  • The transparencies should be decimal numbers between 0 and 1.

  • The x and y coordinates of the points should be decimal numbers ranging from 5 to 10.

Sample Output

In this plot, there are green circular points of varying sizes and transparency.

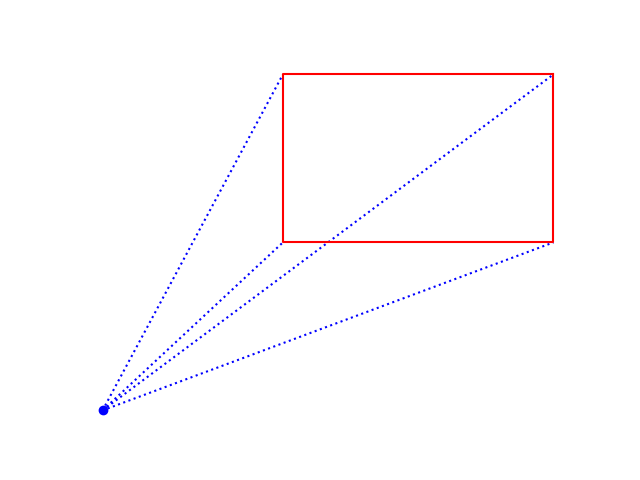
Question-8: Pyramid#

Write a function that takes five parameters representing:

  1. The x-coordinate of the right upper corner of the rectangle.

  2. The y-coordinate of the right upper corner of the rectangle.

  3. The width of the rectangle.

  4. The length of the rectangle.

  5. The color of the rectangle.

The function should:

  • Plot the corresponding rectangle.

  • Plot the point (0,0) in blue color.

  • Draw four dotted blue lines from the point (0,0) to each corner of the rectangle.

  • Remove the axis.

Sample plot:

In this plot, there is a blue point, a red rectangle, and four dashed lines extending from the blue point to each corner of the rectangle.

Question-9: Equation of a Line#

Write a function that takes four parameters representing:

  1. The x-coordinate of the first point.

  2. The y-coordinate of the first point.

  3. The x-coordinate of the second point.

  4. The y-coordinate of the second point.

The function should return the equation of the line that passes through these two points using the slope-intercept form \(y=mx+b\) , where:

  • \(m\) is the slope, calculated as \(m=\frac{y_2-y_1}{x_2-x1}\)

  • \(b\) is the y-intercept, calculated as \(b = y_2 - mx_2\).

Warning: If \(x_2=x_1\) , the equation of the line is \(x=x_2\).

Question-10: Pitch Monitor#

Write a function that takes a list of whole numbers representing pitches and visualize the pitches, using the print() function and * characters.

  • The length of the pitch list is the number of * columns.

  • The numbers in the list represent the number of * characters in each column.

  • For example, if pitch_list = [2, 5, 3, 4], then:

    • The first column has 2 stars.

    • The second column has 5 stars.

    • The third column has 3 stars.

    • The fourth column has 4 stars.

Sample Output for pitch_list = [2,5,3,4]:

There are 4 columns of stars arranged in 5 rows.In the first column, there are 3 spaces followed by 2 stars.In the second column, there are 5 stars.In the third column, there are 2 spaces followed by 3 stars.In the last column, there is 1 space followed by 4 stars.