App: Statistics Module

The statistics module provides most commonly used statistical functions.

• First, you need to import the statistics module.

import statistics

You can access the list of methods in the statistics module by using the dir(statistics) function.

• You can execute help(statistics) for more details.

print(dir(statistics))

['Counter', 'Decimal', 'Fraction', 'LinearRegression', 'NormalDist', 'StatisticsError', '_SQRT2', '__all__', '__annotations__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__spec__', '_coerce', '_convert', '_decimal_sqrt_of_frac', '_exact_ratio', '_fail_neg', '_float_sqrt_of_frac', '_integer_sqrt_of_frac_rto', '_isfinite', '_mean_stdev', '_normal_dist_inv_cdf', '_sqrt_bit_width', '_ss', '_sum', 'bisect_left', 'bisect_right', 'correlation', 'covariance', 'defaultdict', 'erf', 'exp', 'fabs', 'fmean', 'fsum', 'geometric_mean', 'groupby', 'harmonic_mean', 'hypot', 'linear_regression', 'log', 'math', 'mean', 'median', 'median_grouped', 'median_high', 'median_low', 'mode', 'mul', 'multimode', 'namedtuple', 'numbers', 'pstdev', 'pvariance', 'quantiles', 'random', 'reduce', 'repeat', 'sqrt', 'stdev', 'sys', 'tau', 'variance']

Methods

mean()

It returns the mean (average) of the provided data.

data = [1,2,3,3,4,4,4,5,5,6]
print(statistics.mean(data))

3.7

median()

It returns the median of the provided data.

data = [1,2,3,3,4,4,4,5,5,6]
print(statistics.median(data))

4.0

mode()

It returns the mode (most frequent element) of the provided data.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.mode(data))

3

pstdev()

It returns the population standard deviation of the given data.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.pstdev(data))

1.42828568570857

stdev()

It returns the sample standard deviation of the given data.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.stdev(data))

1.505545305418162

pvariance()

It returns the population variation of the given data.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.pvariance(data))

2.04

variance()

It returns the sample variation of the given data.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.variance(data))

2.2666666666666666

quantiles()

It returns three points that divide the data into four intervals, each containing approximately 25 percent of the data.

• The parameter n specifies the number of intervals, with a default value of 4.

data = [1,2,3,3,3,4,4,5,5,6]
print(statistics.quantiles(data))

[2.75, 3.5, 5.0]

data = [1,2,3,4,5,6,7,8,9,10]
print(statistics.quantiles(data))

[2.75, 5.5, 8.25]

correlation()

It returns the Pearson’s correlation coefficient of two given data.

• By default, it computes Pearson’s correlation coefficient, a value ranging between -1 and +1, indicating the strength and direction of a linear relationship between variables.

data1 = [1,2,3,3,3,4,4,5,5,6]
data2 = [4,3,3,2,2,2,3,3,3,1]
print('Pearson’s correlation       coefficient:', statistics.correlation(data1, data2))

Pearson’s correlation       coefficient: -0.5776155346615539

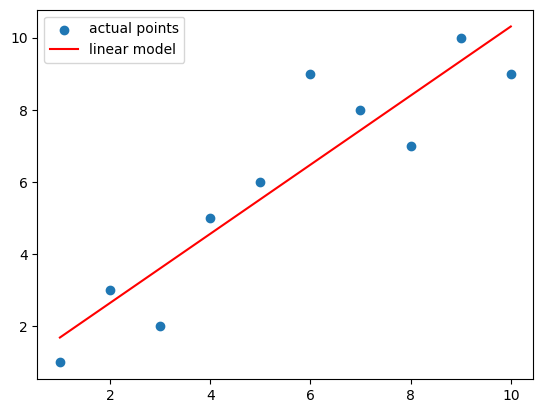
linear_regression()

It returns and returns the slope and intercept of the linear regression model, representing the closest line to the scatter plot of the data.

x = [1,2,3,4,5,6,7,8,9,10]
y = [1,3,2,5,6,9,8,7,10,9]

model = statistics.linear_regression(x, y)
slope = model.slope
intercept = model.intercept

import matplotlib.pyplot as plt
plt.scatter(x,y, label='actual points')

x1, y1 = 1, 1*slope+intercept
x2, y2 = 10, 10*slope+intercept

plt.plot([x1, x2], [y1, y2], color='r', label='linear model')
plt.legend();

sqrt()

It is the square root function. The syntax is statistics.sqrt()

statistics.sqrt(36)

6.0

log()

It returns the logarithm of the given value to the specified base, which defaults to \(e\).

# log base e
statistics.log(1)

0.0

# log base 10
statistics.log(1000, 10)

2.9999999999999996

# log base 2
statistics.log(32, 2)

5.0