Scaling

Machine learning algorithms that rely on the distance between data points require scaled data. Scaling the data ensures that all features are on the same scale.

Minmax Scaler

Scales Values

• Transforms data values to a range between 0 (min) and 1 (max).

Formula

• \(\displaystyle scaled(data) =\frac{data-min}{max-min}\)

​Ensure that both training and test data are scaled in the same way using the min and max of training data.

# data
data = [[1],[2],[3],[4],[5]]

# import MinMaxScaler
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(data)

MinMaxScaler()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# transform data
scaler.transform(data)

array([[0.  ],
       [0.25],
       [0.5 ],
       [0.75],
       [1.  ]])

# transform 2.5
scaler.transform([[2.5]])

array([[0.375]])

Data

from sklearn.datasets import load_breast_cancer
X, y = load_breast_cancer(return_X_y=True)

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

scaler = MinMaxScaler()

# apply min_max_scaler to training and test set
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled  = scaler.transform(X_test)

# original first training data
X_train[0]

array([1.289e+01, 1.312e+01, 8.189e+01, 5.159e+02, 6.955e-02, 3.729e-02,
       2.260e-02, 1.171e-02, 1.337e-01, 5.581e-02, 1.532e-01, 4.690e-01,
       1.115e+00, 1.268e+01, 4.731e-03, 1.345e-02, 1.652e-02, 5.905e-03,
       1.619e-02, 2.081e-03, 1.362e+01, 1.554e+01, 8.740e+01, 5.770e+02,
       9.616e-02, 1.147e-01, 1.186e-01, 5.366e-02, 2.309e-01, 6.915e-02])

# scaled first training data
X_train_scaled[0]

array([0.2546158 , 0.11531958, 0.24164177, 0.14824509, 0.15274894,
       0.06133142, 0.0529522 , 0.0582008 , 0.09076348, 0.12320977,
       0.01510049, 0.02404526, 0.01686849, 0.01097875, 0.10259374,
       0.0841019 , 0.04171717, 0.11185831, 0.15506365, 0.04098089,
       0.18061545, 0.09381663, 0.16730212, 0.0876836 , 0.16973443,
       0.0959906 , 0.1234388 , 0.18439863, 0.14665878, 0.11961682])

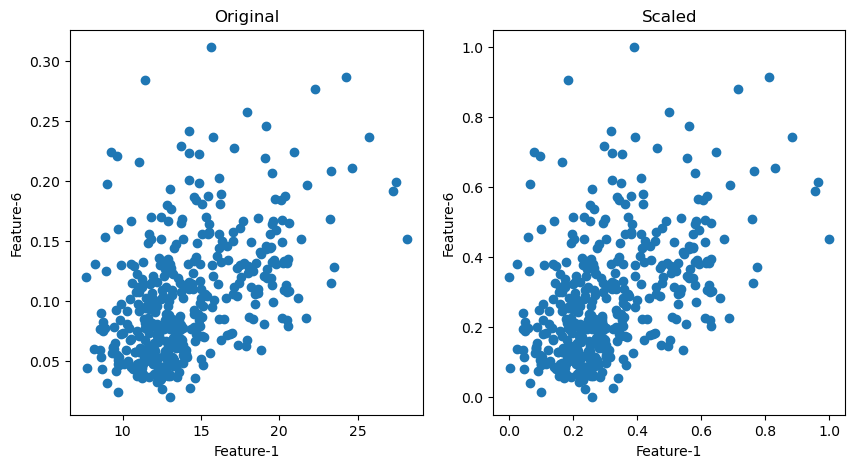
# effect of scaling 1st and 6th ones
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
plt.title('Original')
plt.scatter(X_train[:,0], X_train[:,5])
plt.xlabel('Feature-1')
plt.ylabel('Feature-6')
plt.subplot(1,2,2)
plt.title('Scaled')
plt.scatter(X_train_scaled[:,0], X_train_scaled[:,5])
plt.xlabel('Feature-1')
plt.ylabel('Feature-6')
plt.tight_layout;

kNN with scaled data

# knn classifier applied to the original data
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X_train, y_train)
knn.score(X_train,y_train), knn.score(X_test,y_test)

(0.9507042253521126, 0.9300699300699301)

# knn classifier applied to the scaled data
knn.fit(X_train_scaled, y_train)
knn.score(X_train_scaled, y_train), knn.score(X_test_scaled, y_test)

(0.9906103286384976, 0.972027972027972)